近日，9778818威尼斯研究团队在流体力学研究领域的顶级期刊《Journal of Fluid Mechanics》（简称JFM，剑桥大学出版社旗下核心期刊之一，是流体力学领域的旗舰期刊）上发表了题为“Finite-amplitude instability of the buoyancy boundary layer in a thermally stratified medium”的原创性研究成果（J. Fluid Mech. 2022, vol. 947, A40）。土建学院助理研究员肖越是论文第一作者，工程力学专业2018级本科生李熠、土建学院赵茉莉副教授为合作研究者，王少伟教授为通讯作者。9778818威尼斯是该论文的唯一完成单位。

在自然对流现象中，加热平板置于温度分层流体中会形成浮力边界层，边界层的流动稳定性是流体力学领域的关键问题之一。在各类流动中，从层流到湍流的转捩总以层流的失稳为起点，边界层的转捩会增强流动中的动量交换，从而提高壁面的换热效率、强化换热。浮力边界层的转捩失稳机制在工业生产中扮演着关键角色，有重要的研究价值。对于加热的垂直或倾斜平板上的自然对流，表面的温度分布和周围介质中的热分层决定了流场的主要特征，并在产生不稳定性中起重要作用。先前的研究主要集中在浮力边界层的线性稳定性方面，对于非线性稳定性的研究则较为缺乏。

该论文在国家自然科学基金项目的支持下，通过有限幅值展开方法研究了热分层流体中浮力驱动边界层的弱非线性不稳定性。理论分析表明，不同温度梯度比λ和普朗特数Pr对应着不同的分叉模式。当0≤λ<2，Pr≤2800时，流动呈现超临界分岔。与先前研究结果不同的是，当温度梯度比和普朗特数较大时，系统会出现亚临界分岔（图1）。此外，通过剖析朗道系数中非线性项的贡献，探究了平均流的修正项和速度二次谐波与温度线性模态的相互作用，结果表明该相互作用在亚临界分岔中起着重要作用。基于朗道方程，文中对非线性平衡解的阈值振幅进行了讨论。以上这些研究结论将会促进学者们对浮力驱动的流动系统转捩过程的理解。

近年来，该课题组面向流体力学领域的重要基础问题，在流体的流动与稳定性的力学机理方面连续发表了数篇有影响力的研究成果：Phys. Rev. E 106, 035102 (2022); Phys. Fluids 34, 094102 (2022); Phys. Fluids 34, 044109 (2022); Phys. Fluids 34, 073109 (2022); Phys. Fluids 33, 123113 (2021); Phys. Fluids 33, 033101 (2021)。

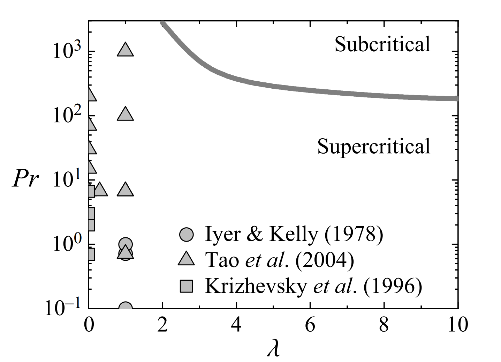
图1. 不同温度梯度比λ和普朗特数Pr对应的分叉模式

论文链接：https://doi.org/10.1017/jfm.2022.685